Regression case: Assessing model agreement in wheat grain nitrogen content prediction

1. Introduction

The metrica package was developed to visualize and compute the level of agreement between observed ground-truth values and model-derived (e.g., mechanistic or empirical) predictions.

This package is intended to fit into the following workflow:

a data set containing the observed values is used to train a model
the trained model is used to generate predictions
a data frame containing at least the observed and model-predicted values is created
metrica package is used to compute goodness of fit and error metrics based on observed and predicted values
metrica package is used to visualize model fit and selected fit metrics

This vignette introduces the functionality of the metrica package applied to observed and model-predicted values of wheat grain nitrogen (N) content (in grams of N \(m^{-2}\)).

2. Wheat grain N content

Let’s begin by loading the packages needed.

library(ggplot2)
library(dplyr)
library(metrica)

Now we load the wheat data set included in the metrica package.

# Load
data(wheat)

# Printing first observations
head(wheat)
#>        pred    obs
#> 1  2.577314  2.544
#> 2  3.989590  4.831
#> 3  5.645253  6.121
#> 4 13.125101 10.960
#> 5  4.955917  5.767
#> 6  6.687800  8.222

This data set contains two columns:

pred: model-predicted wheat grain N content, in g N \(m^{-2}\),
obs: ground-truth observed wheat grain N content, in g N \(m^{-2}\)

3. Visual assessment of agreement

3.1 Scatterplot of pred vs. obs

The simplest way to visually assess agreement between observed and predicted values is with a scatterplot.

We can use the function scatter_plot() from the metrica package to create a scatterplot.

The function requires specifying at least:

the data frame object name (data argument)
the name of the column containing observed values (obs argument)
the name of the column containing predicted values (pred argument)

Besides a scatterplot, this function also adds to the plot the 1:1 line (solid line) and the linear regression line (dashed line).

scatter_plot(data = wheat, 
             obs = obs, 
             pred = pred)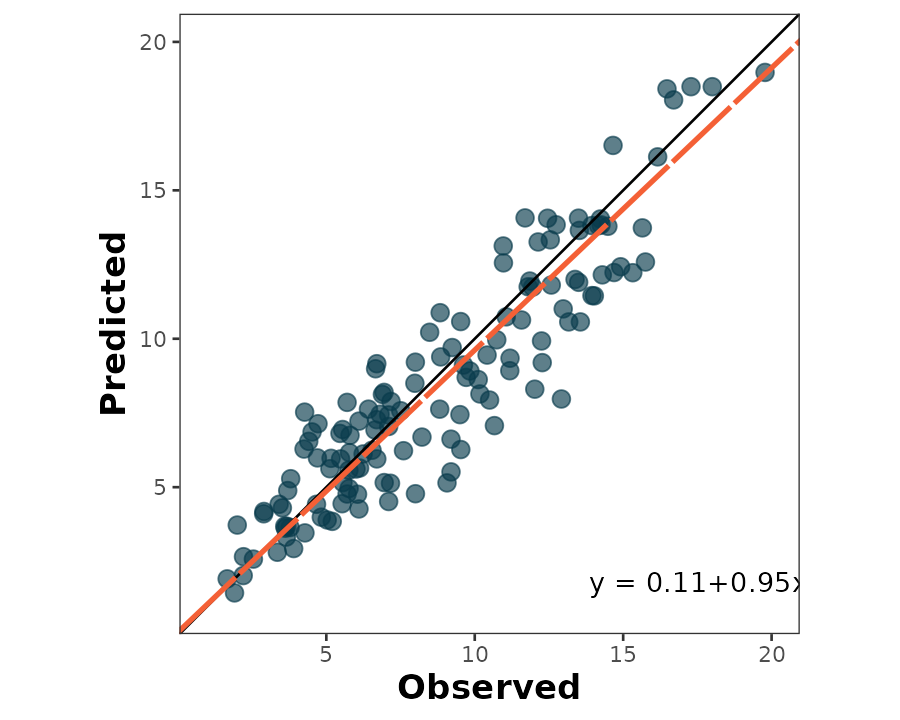

The default behavior of scatter_plot() places the obs column on the x axis and the pred column on the y axis (orientation = "PO"). This can be inverted by changing the argument orientation to “OP”:

scatter_plot(data = wheat, 
             obs = obs, 
             pred = pred,
             orientation = "OP")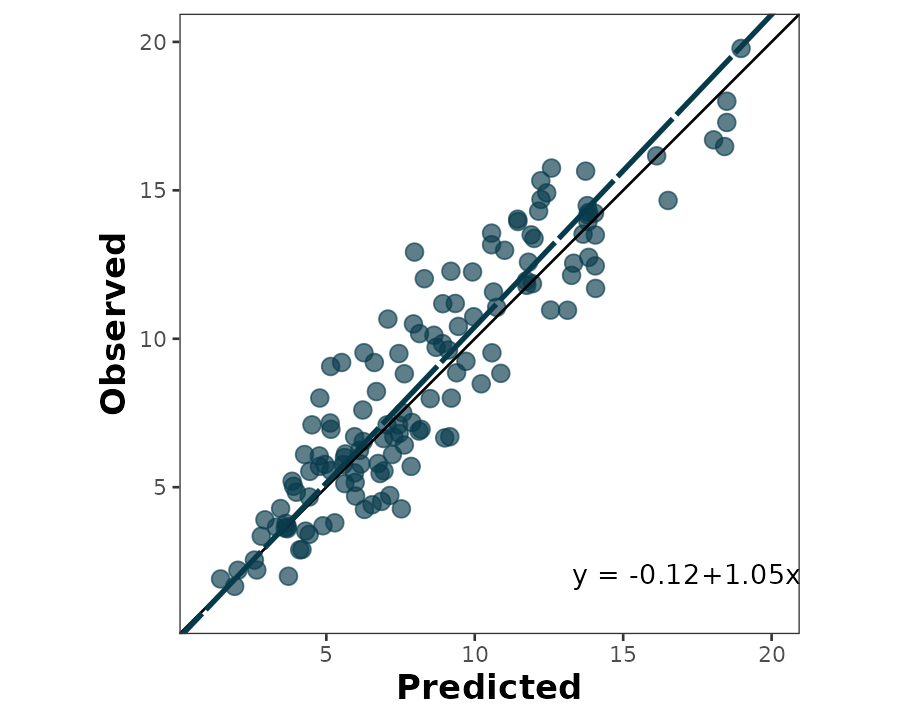

The output of the scatter_plot() function is a ggplot2 object that can be further customized:

scatter_plot(data = wheat, 
             obs = obs, 
             pred = pred,
             orientation = "OP",
             regline_color = "#d0f4de",
             shape_color = "#80ed99",
             eq_color = "white",
             )+
  labs(x ="Predicted wheat N content (g N/m2)",
       y = "Observed wheat N content (g N/m2)")+
  theme_dark()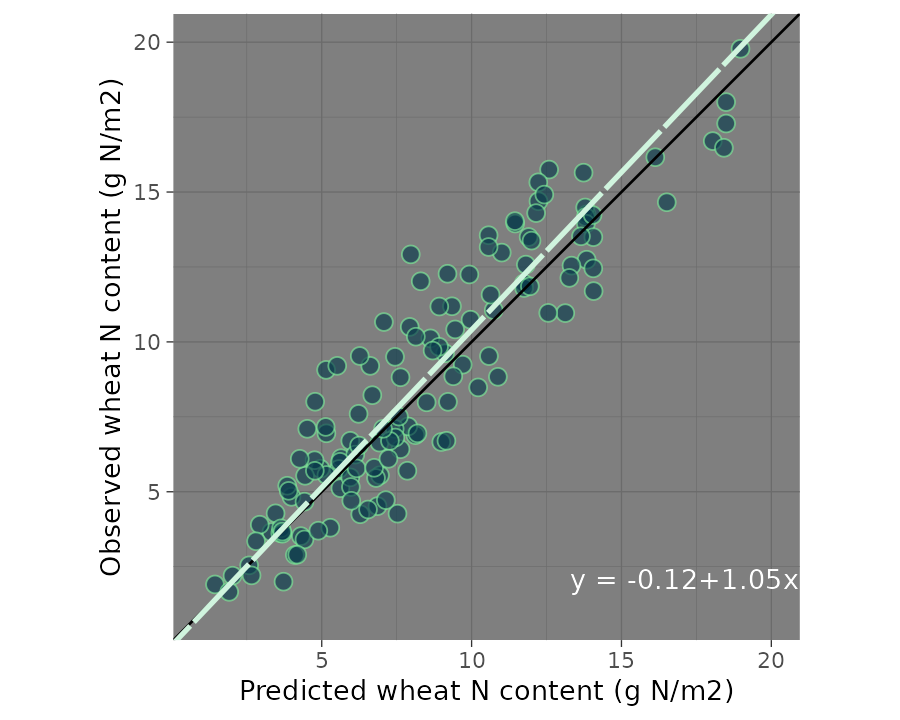

3.2 Bland-Altman plot

The Bland-Altman plot is another way of visually assessing observed vs. predicted agreement. It plots the difference between observed and predicted values on the y axis, and the observed values on the x axis:

bland_altman_plot(data = wheat,
                  obs = obs, 
                  pred = pred)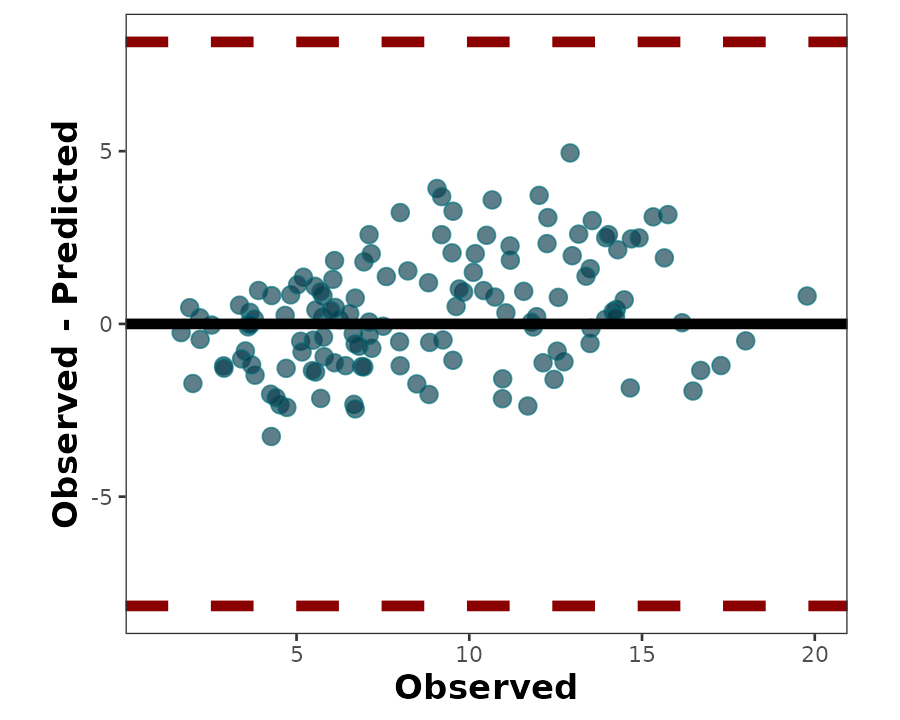

4. Numerical assessment of agreement

The metrica package contains functions for 41 metrics to assess agreement between observed and predicted values for continuous data (i.e., regression error).

A list with all the the metrics including their name, definition, details, formula, and function name, please check [here].

All of the metric functions take the same three arguments as the plotting functions:

the data frame object name (data argument)
the name of the column containing observed values (obs argument)
the name of the column containing predicted values (pred argument)

The user can choose to calculate a single metric, or to calculate all metrics at once.

To calculate a single metric, the metric function can be called.
For example, to calculate \(R^{2}\), we can use the R2() function:

R2(data = wheat,
   obs = obs, 
   pred = pred, tidy = TRUE)
#>          R2
#> 1 0.8455538

Similarly, to calculate root mean squared error, we can use the RMSE() function:

RMSE(data = wheat, 
     obs = obs, 
     pred = pred)
#> $RMSE
#> [1] 1.666441

The user can also calculate all 41 metrics at once using the function metrics_summary():

metrics_summary(data = wheat,
                obs = obs, 
                pred = pred, 
                type = "regression")
#>    Metric       Score
#> 1      B0  0.11315564
#> 2      B1  0.95057797
#> 3       r  0.91953997
#> 4      R2  0.84555376
#> 5      Xa  0.99564191
#> 6     CCC  0.91553253
#> 7     MAE  1.32781184
#> 8    RMAE  0.15214665
#> 9    MAPE 17.51424366
#> 10  SMAPE 17.43518492
#> 11    RAE  0.37156585
#> 12    RSE  0.16128874
#> 13    MBE  0.31815953
#> 14    PBE  3.64561486
#> 15    PAB  3.64510277
#> 16    PPB  1.51438787
#> 17    MSE  2.77702701
#> 18   RMSE  1.66644142
#> 19  RRMSE  0.19094834
#> 20    RSR  0.09678632
#> 21 iqRMSE  0.25237725
#> 22    MLA  0.14328045
#> 23    MLP  2.63374656
#> 24   RMLA  0.14328045
#> 25   RMLP  2.63374656
#> 26     SB  0.10122549
#> 27   SDSD  0.04205496
#> 28    LCS  2.63374656
#> 29    PLA  5.15949064
#> 30    PLP 94.84050936
#> 31     Ue 94.84050936
#> 32     Uc  1.51438787
#> 33     Ub  3.64510277
#> 34    NSE  0.83871126
#> 35     E1  0.62843415
#> 36   Erel  0.77057561
#> 37    KGE  0.91064709
#> 38      d  0.95632264
#> 39     d1  0.80649196
#> 40    d1r  0.81421707
#> 41    RAC  0.95770115
#> 42     AC  0.84174217
#> 43 lambda  0.91553253
#> 44  dcorr  0.89747940
#> 45    MIC  0.78940412

If the user wants just specific metrics, within the same function metrics_summary(), user can pass a list of desired metrics using the argument “metrics_list” as follows:


my.metrics <- c("R2","MBE", "RMSE", "RSR", "NSE", "KGE", "CCC")

metrics_summary(data = wheat,   
                obs = obs,    
                pred = pred,
                type = "regression",
                metrics_list = my.metrics) 
#>   Metric      Score
#> 1     R2 0.84555376
#> 2    CCC 0.91553253
#> 3    MBE 0.31815953
#> 4   RMSE 1.66644142
#> 5    RSR 0.09678632
#> 6    NSE 0.83871126
#> 7    KGE 0.91064709

5. Time series

5.1. Example of timeseries prediction

In some cases, we may count with time-series predictions (e.g. cumulative values from daily simulations). For example, let’s say that we evaluate the production of drymass during the season. For this specific case, the Mean Absolute Scaled Error is a more solid metric compared to conventional RMSE or similar metrics.

Let’s suppose that we have predictions of wheat grain N over the years on the same location for a series of 20 years from 2001 to 2020. Thus, we may get a random sample from the wheat data set and assume they represent the time series of interest. Therefore, we create a new time variable called Year that will serve to sort the observations.

set.seed(165)

wheat_time <- metrica::wheat %>% sample_n(., size = 20) %>% 
  mutate(Year = seq(2001,2020, by =1)) 

# Plot
wheat_time %>% ggplot2::ggplot(aes(x = Year))+
  geom_point(aes(y = pred, fill = "Predicted", shape = "Predicted"))+
  geom_point(aes(y = obs, fill = "Observed", shape = "Observed"))+
  geom_line(aes(y = pred, col = "Predicted", linetype = "Predicted"), size = .75)+
  geom_line(aes(y = obs, col = "Observed", linetype = "Observed"), size = .75)+
  scale_fill_manual(name = "", values = c("dark red","steelblue"))+
  scale_shape_manual(name = "", values = c(21,24))+
  scale_color_manual(name = "", values = c("dark red","steelblue"))+
  scale_linetype_manual(name = "", values = c(1,2))+
  labs(x = "Year", y = "Wheat Grain N (g/m2)")+
  theme_bw()+
  theme(legend.position = "top")
#> Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
#> ℹ Please use `linewidth` instead.
#> This warning is displayed once every 8 hours.
#> Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
#> generated.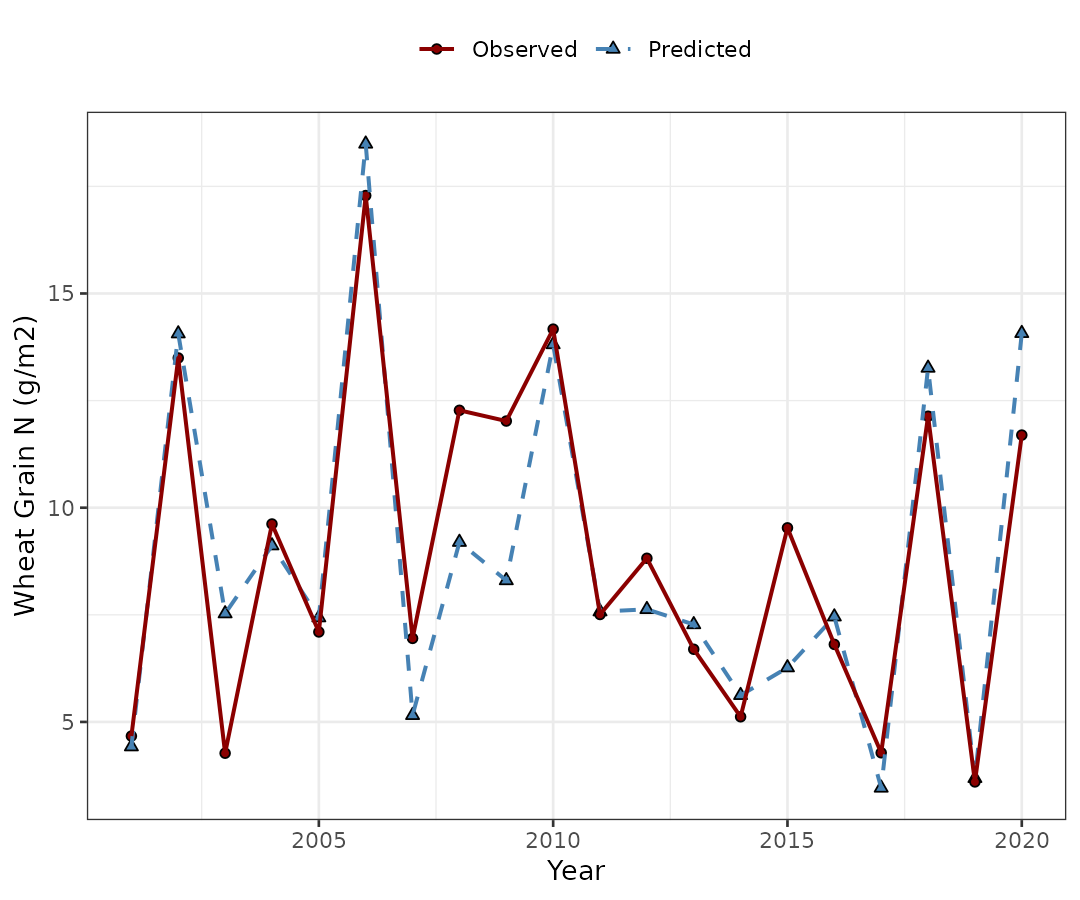

5.2. Use MASE for timeseries

In the case of timeseries analysis, the Mean Absolute Scaled Error (MASE, Hyndman & Koehler, 2006), a scaled error metric, is preferable over other classic metrics such as the RMSE. With metrica, we can use the function MASE. Please, be aware that MASE requires the obs and pred data along with a third column corresponding to the temporal variable that sorts the data (use the time argument to specify it). The default method to scale the MASE is the naive forecast (random-walk), which requires the user to define the size of the naive_step. Otherwise, an out-of-bag MAE can be specified with the oob_mae argument.


# MASE estimate, with naive approach (random-walk, i.e. using observation of t-1 as prediction)
metrica::MASE(data = wheat_time, obs = obs, pred = pred, 
              naive_step = 1, tidy = FALSE, time = "Year")
#> $MASE
#> [1] 0.2444194


metrica::MASE(data = wheat_time, obs = obs, pred = pred, 
              naive_step = 1, tidy = FALSE)
#> $MASE
#> [1] 0.2444194


# MASE estimate, with mae coming from an independent training set.
metrica::MASE(data = wheat_time, obs = obs, pred = pred, 
              naive_step = 1, tidy = FALSE, time = "Year", oob_mae = 6)
#> $MASE
#> [1] 0.2143599

6. Visual and numerical assessment combined

The user can also create a scatter plot that includes not only the predicted vs. observed points, 1:1 line, and regression line, but also selected metrics and their values plus the SMA regression equation.

This is accomplished with the function scatter_plot():

scatter_plot(data = wheat,
             obs = obs, 
             pred = pred)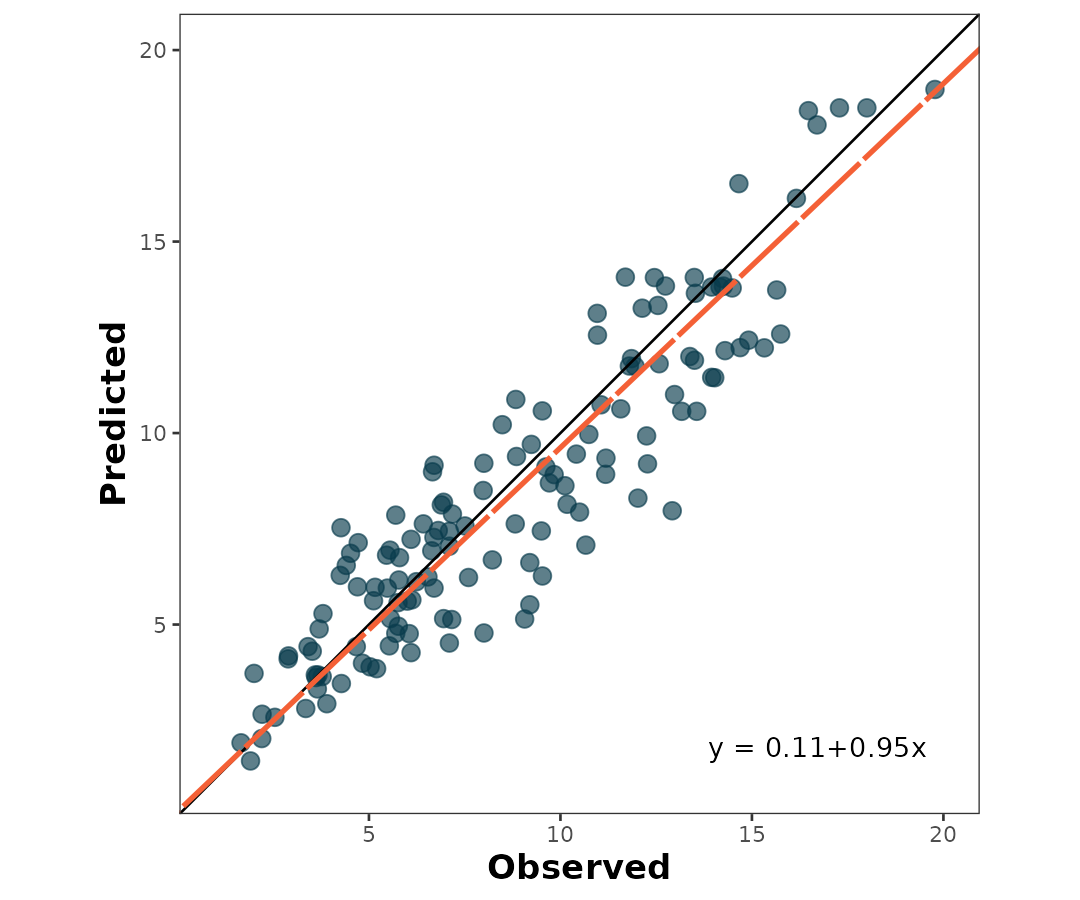

To print the metrics on the scatter_plot(), just use print.metrics. Warning: do not forget to specify your ‘metrics.list’:


my.metrica.plot <- scatter_plot(data = wheat,
                                obs = obs, 
                                pred = pred,
                                print_metrics = TRUE, metrics_list = my.metrics)

my.metrica.plot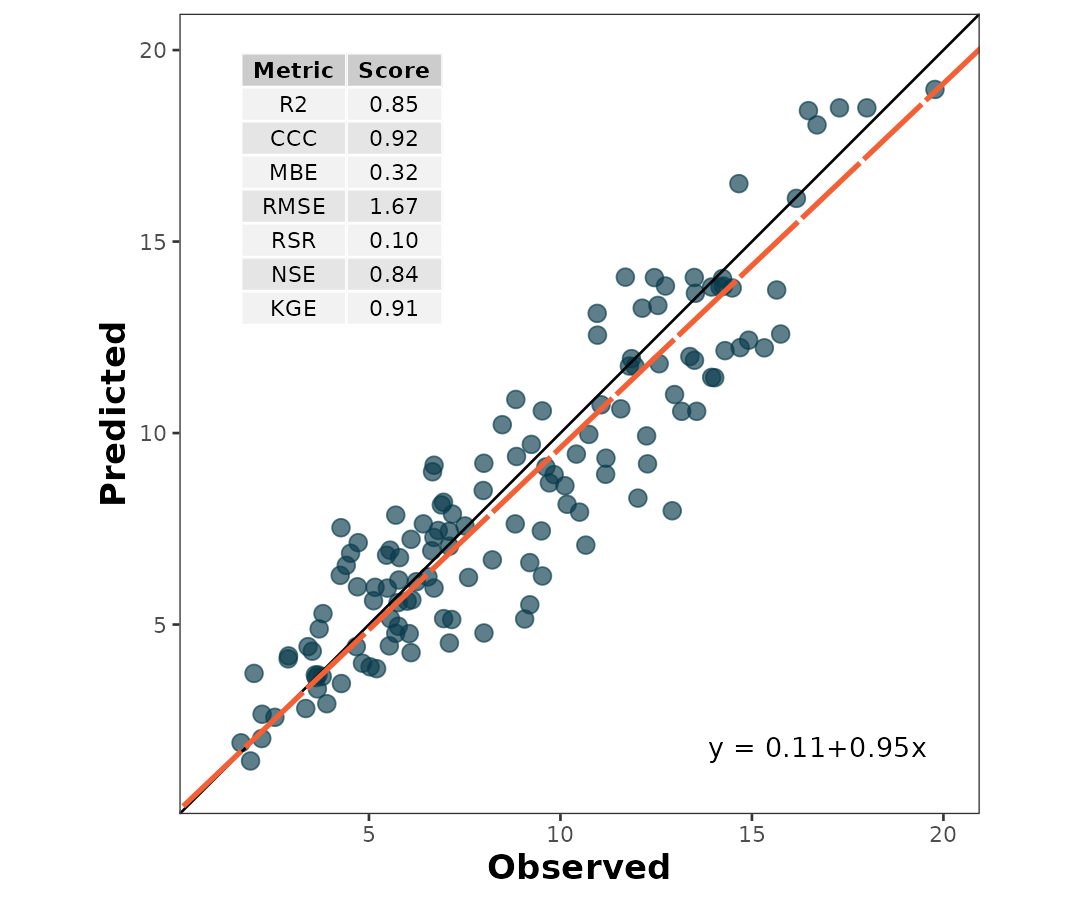

Also, as a ggplot element, outputs are flexible of further edition:


my.metrica.plot +
  # Modify labels
  labs(x = "Observed (days to emergence)", y = "Predicted (days to emergence)")+
  # Modify theme
  theme_light()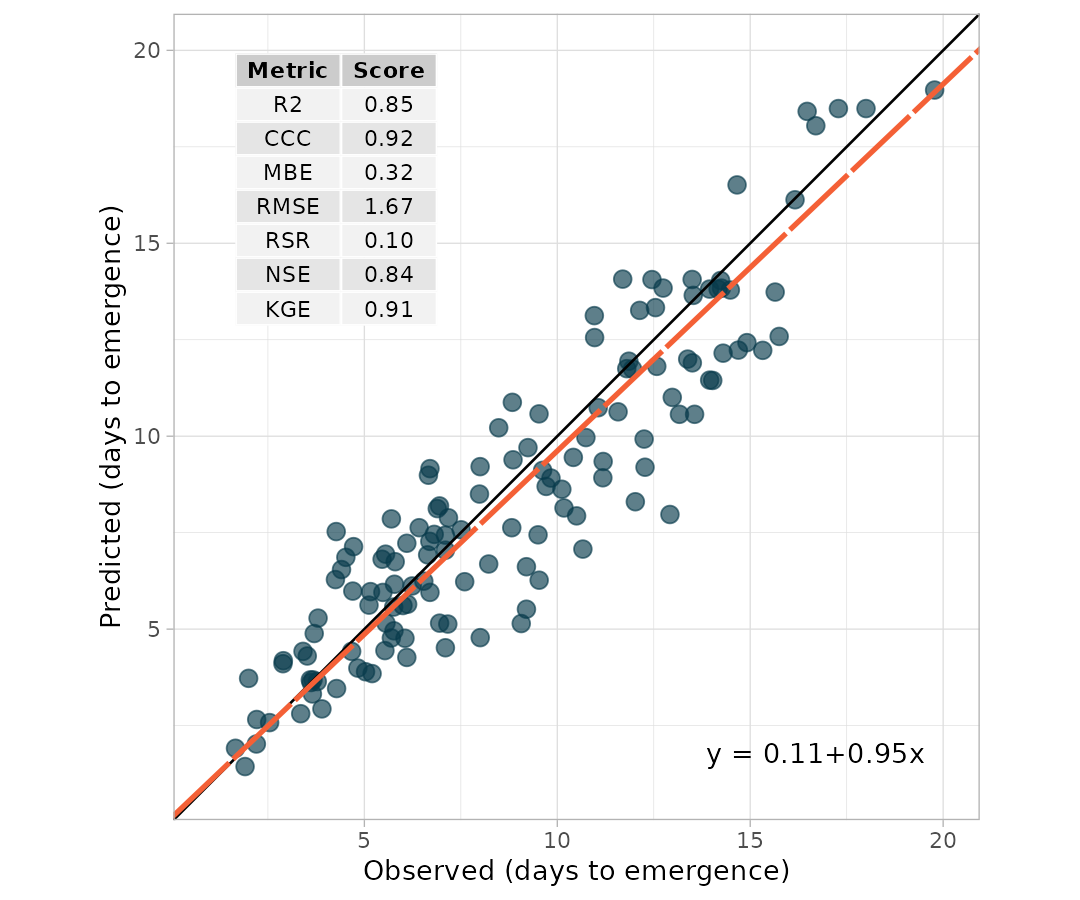


my.metrica.plot +
  # Modify labels
  labs(x = "Observed (Mg/ha)", y = "Predicted (Mg/ha)")+
  # Modify theme
  theme_dark()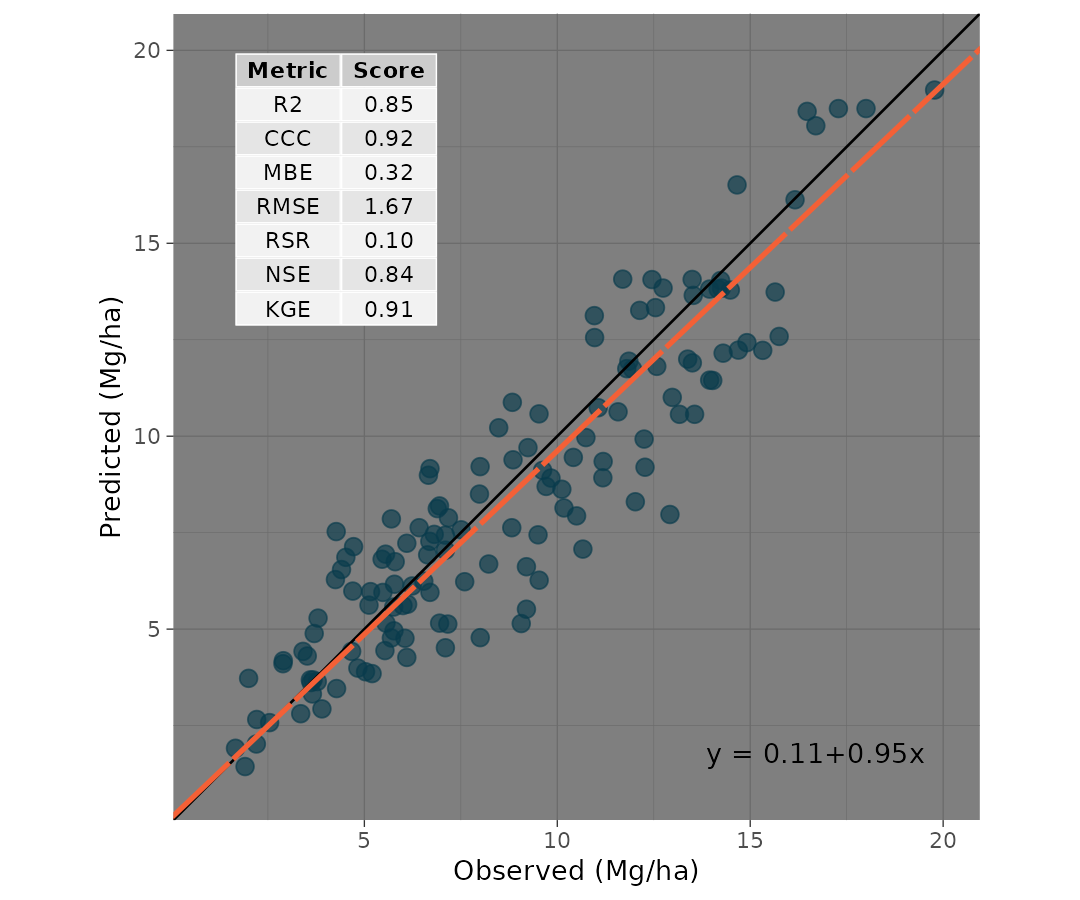

7. Exporting

To export the metrics summary table, the user can simply write it to file with the function write.csv():

metrics_summary(data = wheat,
                obs = obs, 
                pred = pred,
                type = "regression") %>%
  write.csv("metrics_summary.csv")

Similarly, to export a plot, the user can simply write it to file with the function ggsave():


ggsave(plot = my.metrica.plot,
       "scatter_metrics.png",
       width = 5,
       height = 5)

Leo Bastos & Adrian Correndo

2024-06-30